
divide-se uma linha em  partes iguais onde
partes iguais onde  , assim, é sabido que o tamanho dos fragmentos de reta são
, assim, é sabido que o tamanho dos fragmentos de reta são  .
.
 partes iguais onde
partes iguais onde  , assim, é sabido que o tamanho dos fragmentos de reta são
, assim, é sabido que o tamanho dos fragmentos de reta são  .
.
Ao se dividir os lados de um quadrado em  partes iguais, dividimos o quadrado em em
partes iguais, dividimos o quadrado em em  partes iguais. Analogamente, ao se dividir as arestas de um cubo em
partes iguais. Analogamente, ao se dividir as arestas de um cubo em  partes iguais, dividimos o cubo em
partes iguais, dividimos o cubo em 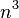 partes iguais.
partes iguais.
 partes iguais, dividimos o quadrado em em
partes iguais, dividimos o quadrado em em  partes iguais. Analogamente, ao se dividir as arestas de um cubo em
partes iguais. Analogamente, ao se dividir as arestas de um cubo em  partes iguais, dividimos o cubo em
partes iguais, dividimos o cubo em 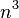 partes iguais.
partes iguais.
Generalizando, se tivermos um hipercubo de  dimensões, este poderá ser dividido em
dimensões, este poderá ser dividido em 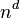 partes iguais ao se dividir a aresta em
partes iguais ao se dividir a aresta em  partes iguais.
partes iguais.
 dimensões, este poderá ser dividido em
dimensões, este poderá ser dividido em 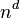 partes iguais ao se dividir a aresta em
partes iguais ao se dividir a aresta em  partes iguais.
partes iguais.
Assim fica demonstrado que na geometria convencional a dimensão é igual ao valor do expoente de n.
Logo, podemos afirmar que  , onde o segmento
, onde o segmento  pode ser afirmado comprimento da linha, e
pode ser afirmado comprimento da linha, e  é definido como o número das partes em que a linha pode ser dividida numa iteração
é definido como o número das partes em que a linha pode ser dividida numa iteração  da construção do fractal, assim,
da construção do fractal, assim,  será o comprimento do segmento na iteração
será o comprimento do segmento na iteração  , onde
, onde  .
.
 , onde o segmento
, onde o segmento  pode ser afirmado comprimento da linha, e
pode ser afirmado comprimento da linha, e  é definido como o número das partes em que a linha pode ser dividida numa iteração
é definido como o número das partes em que a linha pode ser dividida numa iteração  da construção do fractal, assim,
da construção do fractal, assim,  será o comprimento do segmento na iteração
será o comprimento do segmento na iteração  , onde
, onde  .
.
Logo, a dimensão do fractal chamada  será definida ao aplicarmos o logarítmo a ambos membros, ou seja:
será definida ao aplicarmos o logarítmo a ambos membros, ou seja:
 será definida ao aplicarmos o logarítmo a ambos membros, ou seja:
será definida ao aplicarmos o logarítmo a ambos membros, ou seja: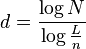 [ logN/N / L [n.....]
[ logN/N / L [n.....]
Nenhum comentário:
Postar um comentário