
geometria indeterminista estocástica.
simbolo de somatoria e integral
x_{n+1}=r_{n}x_{n}(1-x_{n}) [logx/x pP*[a,p,0] [n...........]
simbolo de somatoria e integral
x_{n+1}=r_{n}x_{n}(1-x_{n}) [logx/x pP*[a,p,0] [n...........]
Através dessa função logística ocorre uma oscilação dos valores de r1 , para as variações de a e b, onde temos r_{n}=a +nG ou r_{n}=b+nG, este método propõe o uso de sequências periódicas simples usando símbolos como (a,b), com isso formando padrões na forma (aababba+ nG), está sequência por fim é interpretada através da conversão em código binário (1101001)+ nG.
nG = número de Graceli = [logx/x pP*[a,p,0] [n...........]
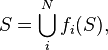 [log i / i [n...]
[log i / i [n...]
Os sistemas de funções iterativas podem ser matematicamente definidos da seguinte maneira:
Seja um espaço  e seu correspondente espaço métrico
e seu correspondente espaço métrico 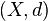 (onde
(onde  é uma métrica para o espaço
é uma métrica para o espaço  ), uma transformação
), uma transformação 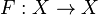 é contrativa (também dito ummapeamento contrativo) se existir um fator de contratividade
é contrativa (também dito ummapeamento contrativo) se existir um fator de contratividade  tal que:
tal que: 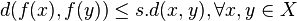 .
.
 e seu correspondente espaço métrico
e seu correspondente espaço métrico 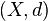 (onde
(onde  é uma métrica para o espaço
é uma métrica para o espaço  ), uma transformação
), uma transformação 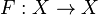 é contrativa (também dito ummapeamento contrativo) se existir um fator de contratividade
é contrativa (também dito ummapeamento contrativo) se existir um fator de contratividade  tal que:
tal que: 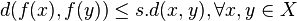 .
.
Um sistema de funções iterativas é um conjunto finito de funções contrativas 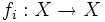 , que pode ser definido também da seguinte forma1 : mais a função variacional Graceli leva o sistema ao indeterminismo transcendente .
, que pode ser definido também da seguinte forma1 : mais a função variacional Graceli leva o sistema ao indeterminismo transcendente .
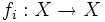 , que pode ser definido também da seguinte forma1 : mais a função variacional Graceli leva o sistema ao indeterminismo transcendente .
, que pode ser definido também da seguinte forma1 : mais a função variacional Graceli leva o sistema ao indeterminismo transcendente .
onde
e
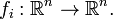
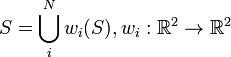 .[ log i / i [n...] [pP] [a,p,0]
.[ log i / i [n...] [pP] [a,p,0]- A forma indeterminística consiste em em escolher um conjunto inicial
 e aplicar as transformações
e aplicar as transformações  nos elementos do conjunto
nos elementos do conjunto  , de forma a gerar um novo conjunto
, de forma a gerar um novo conjunto  , e repetir o mesmo procedimento nos novos conjuntos gerados iterativamente de forma que:
, e repetir o mesmo procedimento nos novos conjuntos gerados iterativamente de forma que: [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0]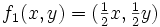 [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0] [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0]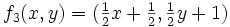 [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0]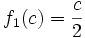 [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0] [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0] [ log i / i [n...] [pP] [a,p,0]
[ log i / i [n...] [pP] [a,p,0]
. As funções que compões este sistema são:Ou ainda, na notação complexa mais comumente usada:

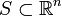
Nenhum comentário:
Postar um comentário